Большая Энциклопедия Нефти и Газа
Максимальное хроматическое число равно 5 для плоского графа. В зависимости от значения к графы именуют х-хроматическими. Над графами могут быть произведены операции расширения в надграф — внедрение некоторых новых вершин в соответствующие ребра, так чтобы эти ребра превратились в цепь, а также сжатия — удаление некоторых вершин и ребер, переводящее граф в другой граф ( подграф), содержащий меньшее их количество. [3]
Хроматическое число конъюнкции GjAGa двух графов Ог и G2 не превосходит хроматических чисел этих графов. [4]
Хроматическое число связного однородного графа степени 2 с п вершинами равно двум, если п четно; 3, если п нечетно. [5]
Хроматическим числом % ( G) графа G называется наименьшее k, при котором G имеет правильную k — раскраску. [6]
Хроматическим числом х ( G) [ реберным х р о м а т и ч в с к-им ч и-е л о м х ( 6) 1 наз — наименьшее количество цветов, к-рыми можно раскрасить вершины ( ребра) графа G так, чтобы любые смежные вершины ( ребра) были окрашены разными цветами. [7]
Хроматическим числом метрического пространства ( X, р), отвечающим запрещенному расстоянию о0, называется величина х ( ( Х, р), а), равная минимальному количеству цветов, в которые можно так раскрасить все множество X, чтобы любые два его элемента, отстоящие друг от друга на расстояние о, оказались раскрашенными в разные цвета. [8]
Нахождение хроматического числа ( так же, как и чисел независимости и доминирования) — это не простая задача, а для некоторых классов графов представляет собой чрезвычайно сложную проблему. [9]
О хроматическом числе произвольного графа мало что можно сказать. Значительного прогресса можно добиться, если известна степень каждой вершины графа. [10]
Утверждение 15.4. Хроматическое число дерева равно 2, так как дерево является двудольным графом. [11]
Нижние оценки хроматического числа безусловно более интересны, чем верхние, поскольку ( если они достаточно близки к истинному значению) они могут быть использованы в процедуре вычисления — у ( С), включающей дерево поиска. В то же время верхние оценки хроматического числа подобного применения не находят. [12]
Нижние оценки хроматического числа безусловно более интересны, чем верхние, поскольку ( если они достаточно близки к истинному значению) они могут быть использованы в процедуре вычисления у ( G), включающей дерево поиска. В то же время верхние оценки хроматического числа подобного применения не находят. [13]
Известна оценка хроматического числа планарных графов . [14]
Общее понятие хроматического числа метрического пространства было предложено в 1976 году Бендой и Перлесом. Однако частные случаи рассматривались существенно раньше: еще в сороковые годы двадцатого века Эрдеш и Хадвигер дали ставшее ныне классическим определение величины x ( Rn) — хроматического числа п — мерного евклидова пространства. За прошедшие с тех пор шестьдесят лет были получены многочисленные результаты как в классической задаче, так и в ее обобщении. [15]
Источник
Оценки хроматического числа
Теорема 3. Граф G с максимальной степенью вершин является s — раскрашиваемым, за исключением двух случаев:
1. при граф содержит компоненту , являющуюся полным графом плотности
2. при граф G содержит компоненту, являющуюся циклом нечетной длины.
Оценки, полученные с помощью этих теорем, дают хорошее приближение лишь тогда, когда степени всех вершин графа имеют близкие значения. В противном случае оценка может быть значительно завышена.
Теорема 4. Для любого графа
где вершинное число независимости графа.
Алгоритм минимальной раскраски вершин графа
1. Выделяем множество пустых подграфов графа G.
2. Строим двумерную таблицу, каждой строке которой сопоставим взаимно однозначно пустой подграф, столбцу – вершину; в клетке записываем единицу, если j-ая вершина содержится в i-ом пустом подграфе, в противном случае клетку оставляем пустой.
3. Определяем покрытия столбцов строками. Каждое покрытие порождает раскраску. Покрытие минимальной мощности определяет хроматическое число графа G.
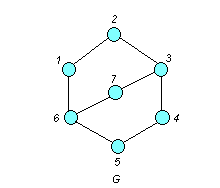
Пример. Определить хроматическое число графа G, изображенного на рис. 5.12
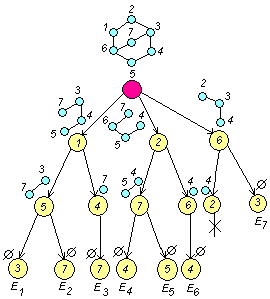
□ Для определения хроматического числа сначала необходимо выделить все пустые подграфы заданного графа G. Используя алгоритм выделения пустых подграфов, построим дерево (рис.5.13).
Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1, 4, 7. Значит
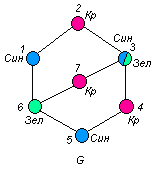
Зададимся красками: для множествами вершин синяя (Син), для множества вершин краска красная ( Кр ), для множества вершин краска зеленая ( Зел ) .
Раскрасим вершины графа G :
Отметим, что вершину 3 можно раскрасить в два цвета: синий или зеленый. ■
Замечание. Аналогично можно определить раскраску ребер графа G и найти минимальную раскраску ребер этого графа G .
§ 7. Планарность графа
Планарность графов играет существенную роль при проектировании коммуникаций и связи между объектами на плоскости: дороги между населенными пунктами, водопроводные и газопроводные сети, линии электропередач, межсоединения на печатных платах и кристаллах интегральных схем и т.д.
Граф называется планарным (плоским ), если существует изоморфный ему граф, который может быть изображен на плоскости без пересечения ребер.
Свойства планарности не нарушаются, если некоторое ребро разбить на два ребра введением вершины второй степени или заменить два ребра, инцидентных вершине второй степени, одним ребром, удалив эту вершину.
Два графа называются гомеоморфными (изоморфными с точностью до вершины второй степени), если после удаления из них вершин второй степени и объединения инцидентных этим вершинам ребер, они оказываются изоморфными.
Граф, гомеоморфный планарному графу, также является планарным.
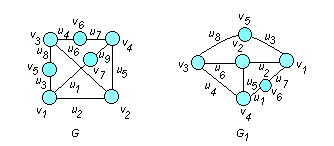
Пример. Являются ли графы G и G1 (рис. 5.14) гомеоморфными?
□ Графы G и G1 являются гомеоморфными, т.к. после удаления в графе G вершин второй степени и объединения инцидентных этим вершинам ребер u3 и u8 , u4 и u7 , u1 и u9 и после удаления в графе G1 вершин второй степени и объединения инцидентных этим вершинам ребер u3 и u8 , u1 и u7 , графы G и G1 оказываются изоморфными ( см. Глава ΙV, рис. 4.4 ). ■
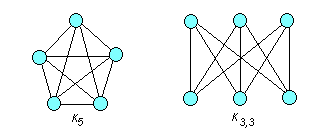
Теорема (Л.С.Понтрягина). Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного К5 или К3,3 .
Граф К5 – минимальный полный граф, который не является планарным (рис. 5.15). Удаление одного ребра делает этот граф планарным.
Граф К3,3 – минимальный полный двудольный граф, который не является планарным (рис. 5.15). Удаление одного ребра делает этот граф планарным.
Толщиной графа G называется наименьшее число планарных графов, объединение которых дает граф G.
Толщина планарного графа равна 1.
Нижняя оценка толщины графа определяется неравенством
где ] [ — ближайшее целое число, степень i-ой вершины.
Замечание. Для строгого доказательства планарности графа используется теорема Понтрягина, а указанное неравенство лишь только нижняя оценка толщины графа.
Пример. Является ли граф G (рис. 5.16) планарным? Если нет, то определить, какие ребра необходимо удалить (реализовать на других плоскостях) для преобразования графа G в планарный.
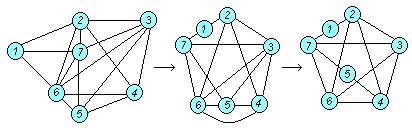
□ Согласно теореме Понтрягина проверяем граф G на содержание подграфа, гомеоморфного К5 .
Проверку можно сделать следующим образом: удаляя минимальное количество вершин и некоторое количество ребер, попытаться привести заданный граф G к виду графа К5 . В приведенном графе могут присутствовать вершины второй степени.
В заданном графе G можно не удалять ни одной из вершин. Преобразования показаны на рис. 5.17
В результате получили подграф, гомеоморфный К5 , т.е. заданный граф G не является планарным. Удаление любого ребра в полученном подграфе делает его (подграф) планарным.
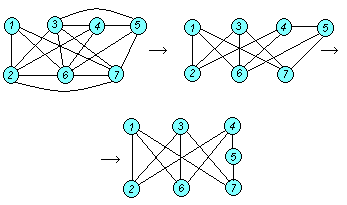
Теперь проверим граф G на содержание подграфа, гомеоморфного К3,3 . Попытаемся привести граф G к виду К3,3 .
В графе К3,3 все вершины имеют степень, равную 3. В графе G степень вершин больше или равна 3, поэтому в процессе преобразования графа G вершины удалять не будем. Сведение графа G к виду графа К3,3 показано на рис. 5.18
В результате получен подграф, гомеоморфный К3,3 . Удаление любого ребра в полученном подграфе делает его планарным.
Вывод: заданный граф G содержит подграфы, гомеоморфные К5 и К3,3. Следовательно, заданный граф G не является планарным.
Определим нижнюю оценку толщины графа G :
Так как удаление любого ребра из каждого полученного подграфа выводит их из класса подграфов, гомеоморфных К5 или К3,3 , то граф G станет планарным, если удалить ребро, входящее как в подграф, гомеоморфный К5 , так и в подграф, гомеоморфный К3,3. Таким множеством общих ребер является множество
Удаление любого из этих ребер делает заданный граф G планарным.
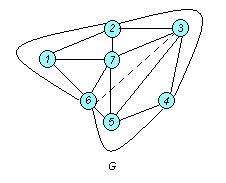
После удаления, например, ребра получаем планарный граф, плоское представление которого изображено на рис. 5.19.
Соединение, которое соответствует удаленному ребру (показано пунктирной линией), реализуется на второй плоскости. Толщина графа G равна двум. ■
Источник